Lineer Cebir
Bu bölümde lineer cebirin temel yapıtaşları olan skalarlar, vektörler, matrisler ve tensörler üzerinde duracağız. Ayrıca, bu yapılar üzerinde yapılabilecek bazı temel işlemleri inceleyeceğiz.
İlk adım olarak, gerekli kütüphaneleri içe aktaralım:
from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import cv2
Veri Yapıları
Bu kısımda farklı veri yapılarını inceleyeceğiz.
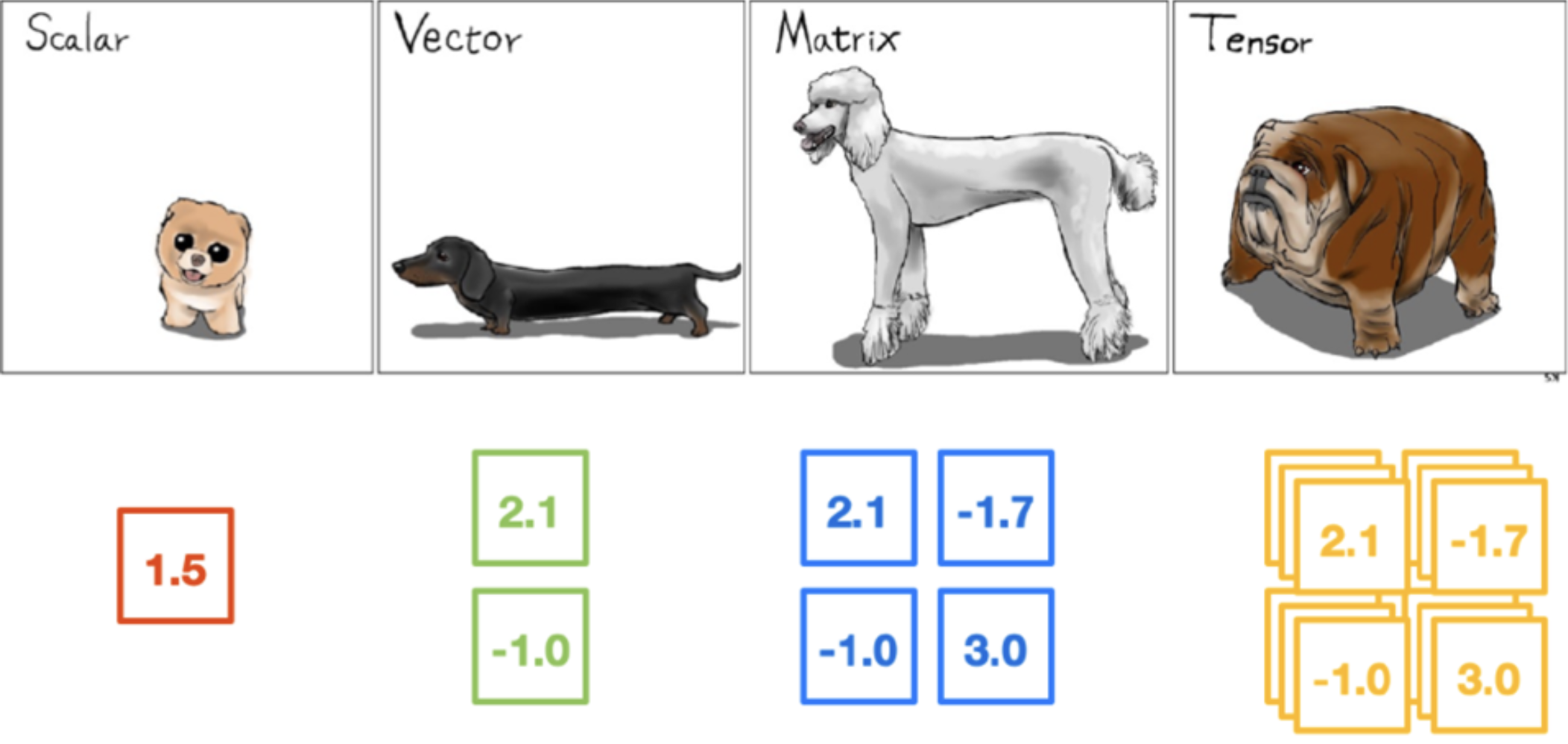
Scalar
Skalar, tek bir sayısal değerdir ve herhangi bir yönü yoktur. Bu, matematiksel işlemlerde sıklıkla kullanılan en basit veri yapısıdır.
scalar = np.array([15])
print("scale boyutu",scalar.ndim)
print("scale:{0}".format(scalar))
print("scale %i"%scalar)
scale boyutu 1
scale:[15]
scale 15
Vector
Vektörler, büyüklük ve yön içeren ve bir dizi şeklinde ifade edilebilen yapılar olarak tanımlanır.
array1 = np.array([1,2,3,4,5],ndmin=2)
array1
array([[1, 2, 3, 4, 5]])
array1.reshape(5,1)
array([[1],
[2],
[3],
[4],
[5]])
array1.shape
(1, 5)
print(f"Type,'Tip': {type(array1)}")
print(f"Shape,'Biçim': {array1.shape}")
print(f"Dimension,'Boyut': {array1.ndim}")
Type,'Tip': <class 'numpy.ndarray'>
Shape,'Biçim': (1, 5)
Dimension,'Boyut': 2
Matrix
Matrisler, iki boyutlu dizilerdir ve lineer cebirde sıkça kullanılırlar.
array2 = np.array([[1,2,3,4],
[5,6,7,8]])
array2
array([[1, 2, 3, 4],
[5, 6, 7, 8]])
print(f"Type,'Tip': {type(array2)}")
print(f"Shape,'Biçim': {array2.shape}")
print(f"Dimension,'Boyut': {array2.ndim}")
Type,'Tip': <class 'numpy.ndarray'>
Shape,'Biçim': (2, 4)
Dimension,'Boyut': 2
Tensor
Tensörler, genellikle görüntü işlemede kullanılan üç veya daha fazla boyutlu dizilerdir.
img = cv2.imread("ML.png",cv2.IMREAD_GRAYSCALE)
plt.imshow(img,cmap="gray")
print(f"Type,'Tip': {type(img)}")
print(f"Shape,'Biçim': {img.shape}")
print(f"Dimension,'Boyut': {img.ndim}")
Type,'Tip': <class 'numpy.ndarray'>
Shape,'Biçim': (600, 1000)
Dimension,'Boyut': 2

Diğer bazı temel tensör işlemleri:
np.zeros((3,3))
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
np.ones((3,3))
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
print(f"2 sayı arasında belirtildiği aralık ile adımlar ile yaklaşılması: {np.arange(2,15,2)}\n"
f"2 sayı arasında belirtilen adım sayısı kadar yaklaşılması: {np.linspace(2, 5, 5)}\n"
f"2 sayı aralığında belirtilen boyutta rastgele bir matris oluştur: \n {np.random.randint(10, 100, size= (3,3))}\n")
2 sayı arasında belirtildiği aralık ile adımlar ile yaklaşılması: [ 2 4 6 8 10 12 14]
2 sayı arasında belirtilen adım sayısı kadar yaklaşılması: [2. 2.75 3.5 4.25 5. ]
2 sayı aralığında belirtilen boyutta rastgele bir matris oluştur:
[[98 12 77][74 69 99]
[31 95 76]]
Matris İşlemleri
Matrisler, lineer cebirde temel yapıtaşlarından biridir ve çeşitli matematiksel işlemler için kullanılırlar. Bu bölümde, matris toplama, çıkarma, çarpma ve bölme işlemleri üzerinde duracağız.
Toplama ve Çıkarma İşlemi
Matris toplama ve çıkarma işlemleri, sadece aynı boyutlara sahip matrisler için tanımlanır. Bu işlemler sırasında, matrislerin karşılıklı elemanları toplanır veya çıkarılır ve sonuç yeni bir matris şeklinde oluşturulur.
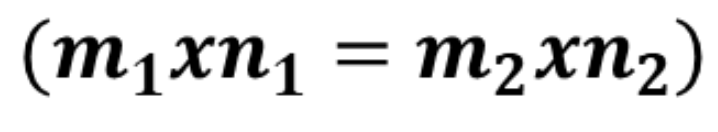
A_matrix = np.random.randint(5,10,size=(5,5))
B_matrix = np.random.randint(4,12,size=(5,5))
A_matrix
array([[9, 8, 5, 5, 6],
[8, 7, 5, 5, 5],
[5, 9, 9, 9, 8],
[5, 9, 5, 5, 9],
[6, 6, 9, 5, 9]])
B_matrix
array([[11, 8, 7, 7, 7],
[10, 4, 5, 8, 10],
[6, 4, 8, 6, 8],
[8, 9, 4, 5, 9],
[8, 5, 4, 6, 4]])
addition_matrix = A_matrix + B_matrix
subtriction_matrix = A_matrix - B_matrix
print(f"toplama işlemi: \n{addition_matrix}\n"
f"#################\n"
f"çıkarma işlemi: \n{subtriction_matrix}")
toplama işlemi:
[[20 16 12 12 13][18 11 10 13 15]
[11 13 17 15 16][13 18 9 10 18]
[14 11 13 11 13]]
#################
çıkarma işlemi:
[[-2 0 -2 -2 -1][-2 3 0 -3 -5]
[-1 5 1 3 0][-3 0 1 0 0]
[-2 1 5 -1 5]]
Çarpma ve Bölme İşlemi
Skaler Çarpım
Skaler çarpım, iki matrisin karşılıklı elemanlarının çarpılması ile elde edilir. Bu işlem sonucu, orijinal matrislerin boyutları korunur.
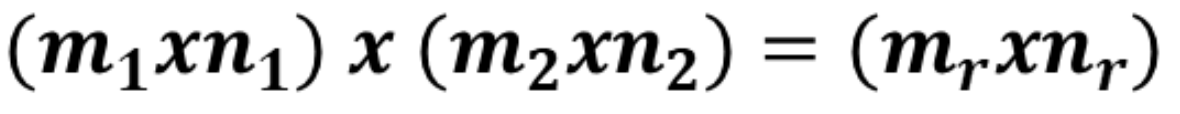
multip = A_matrix * B_matrix
multip
array([[99, 64, 35, 35, 42],
[80, 28, 25, 40, 50],
[30, 36, 72, 54, 64],
[40, 81, 20, 25, 81],
[48, 30, 36, 30, 36]])
multip1 = B_matrix * A_matrix
multip1
array([[99, 64, 35, 35, 42],
[80, 28, 25, 40, 50],
[30, 36, 72, 54, 64],
[40, 81, 20, 25, 81],
[48, 30, 36, 30, 36]])
Vektörel Çarpım (Dot
Product)
Vektörel çarpım, iki matrisin satır ve sütunlarının çarpımlarının toplamı ile elde edilen yeni bir matris oluşturur. Bu işlem için ilk matrisin sütun sayısı ile ikinci matrisin satır sayısının eşit olması gerekir.
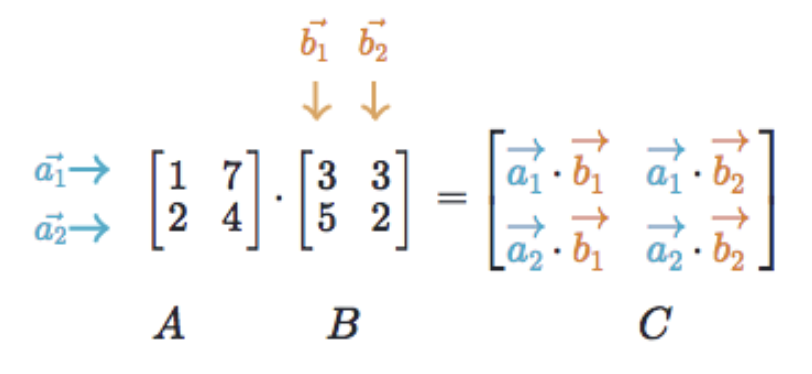
A_matrix.shape
(5, 5)
B_matrix.shape
(5, 5)
dot_product = A_matrix.dot(B_matrix)
dot_product
array([[297, 199, 187, 218, 252],
[268, 182, 171, 197, 231],
[335, 233, 220, 254, 310],
[287, 186, 176, 216, 246],
[292, 198, 200, 223, 255]])
Matris çarpma işlemleri, lineer cebirde önemli bir yer tutar ve çeşitli matematiksel ve fiziksel problemlerin çözümünde kullanılır. Özellikle sistem denklemlerinin çözümleri, matris çarpımı ile elde edilebilir.
Matrislerde Çarpma İşleminin Özellikleri:
Matris çarpımı, belirli kurallara göre gerçekleştirilen bir işlemdir. Aşağıda, matris çarpma işleminin bazı temel özellikleri verilmiştir:
- Değişme Özelliği Yoktur: Matris çarpımı, genelde değişken değildir. Yani, A ve B matrisleri için, genellikle A.B ≠ B.A olur.
- Dağılma Özelliği: A, B ve C matrisleri için, A(B+C) = A.B + A.C eşitliği geçerlidir.
- Birleşme Özelliği: A(B.C) = (A.B)C eşitliği her zaman sağlanır.
- Birim Matris ile Çarpım: Herhangi bir A matrisi için, A.I = I.A = A eşitliği geçerlidir. Burada I, birim matristir.
Bölme İşlemi
Matris bölmesi, genellikle bir matrisin diğer matrisin tersi ile çarpımı şeklinde tanımlanır. Ancak matrisler arasında doğrudan bir bölme işlemi tanımlı değildir; bunun yerine bir matrisin tersinin alınması ve bu ters matris ile çarpım yapılması gerekir.

Bir Matrisin Transpozu
Matrisin transpozu, matrisin satırları ile sütunlarının yer değiştirmesiyle elde edilen yeni bir matristir. mxn boyutundaki bir A matrisinin transpozu ( A^T ) şeklinde gösterilir ve boyutu nxm olur.
Orj_matris = np.array([[3,5,10,4,1],
[4,2,8,4,2],
[8,12,16,4,5]])
Tran_matris = np.transpose(Orj_matris)
print(f"Orjinal matris: \n{Orj_matris}\n"
f"Orjinal matris boyutu: {Orj_matris.shape}\n"
f"Transpoze matris: \n{Tran_matris}\n"
f"Transpoze matris boyutu: {Tran_matris.shape}")
Orjinal matris:
[[ 3 5 10 4 1][ 4 2 8 4 2]
[ 8 12 16 4 5]]
Orjinal matris boyutu: (3, 5)
Transpoze matris:
[[ 3 4 8][ 5 2 12]
[10 8 16][ 4 4 4]
[ 1 2 5]]
Transpoze matris boyutu: (5, 3)
İnverse Matris (Bir matrisin tersini alma)
Bir matrisin tersi, o matrisle çarpıldığında birim matrisi (identity matrix) veren matristir. Her matrisin tersi bulunmaz; sadece kare matrislerin ve determinantı sıfır olmayan matrislerin tersi alınabilir.
,
Bir matrisin tersini almak, özellikle sistem denklemlerinin çözümünde önemlidir.
matrix_1 = np.array(np.ones((2,2))*np.random.randint(5,100,size=(2,2)))
matrix_1
array([[87., 14.],
[25., 26.]])
matrix_2 = np.array(np.ones((3,3))*np.random.randint(5,100,size=(3,3)))
matrix_2
array([[96., 83.,94.],
[61., 24., 92.],
[37., 15., 40.]])
invers_1 = np.linalg.inv(matrix_1)
invers_1
array([[ 0.01359833, -0.00732218],
[-0.01307531, 0.04550209]])
invers_2 = np.linalg.inv(matrix_2)
invers_2
array([[-0.00994554, -0.04522851, 0.12739758],
[ 0.02282737, 0.00857211, -0.07336017],
[ 0.00063936, 0.03862183, -0.0653327 ]])
Birim Matris Elde Edebilecek miyiz??
Identity_1 = matrix_1.dot(invers_1)
Identity_1
array([[1.00000000e+00, 0.00000000e+00],
[5.55111512e-17, 1.00000000e+00]])
Identity_2 = np.dot(matrix_2,invers_2)
Identity_2
array([[ 1.00000000e+00, -6.10622664e-16, 1.11022302e-15],
[-1.55691432e-16, 1.00000000e+00, 1.33226763e-15],
[-1.01481323e-16, -2.22044605e-16, 1.00000000e+00]])
Bu kısımda, matrislerin temel işlemleri, özellikle ters ve transpoze alma gibi işlemler üzerinde durduk. Bu işlemler, matrislerle yapılan daha karmaşık hesaplamaların temelini oluşturur.